正四面体的内切球图片

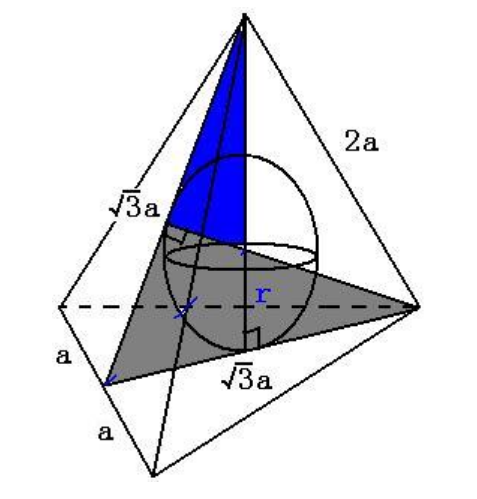
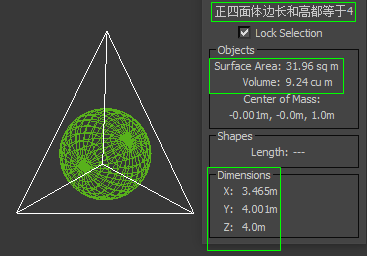
棱长为a时,内切球半径为 r=√6a/12 ∴a=12r/√6=2√6r 设正四面体
图片尺寸477x499
正四面体结论
图片尺寸480x435
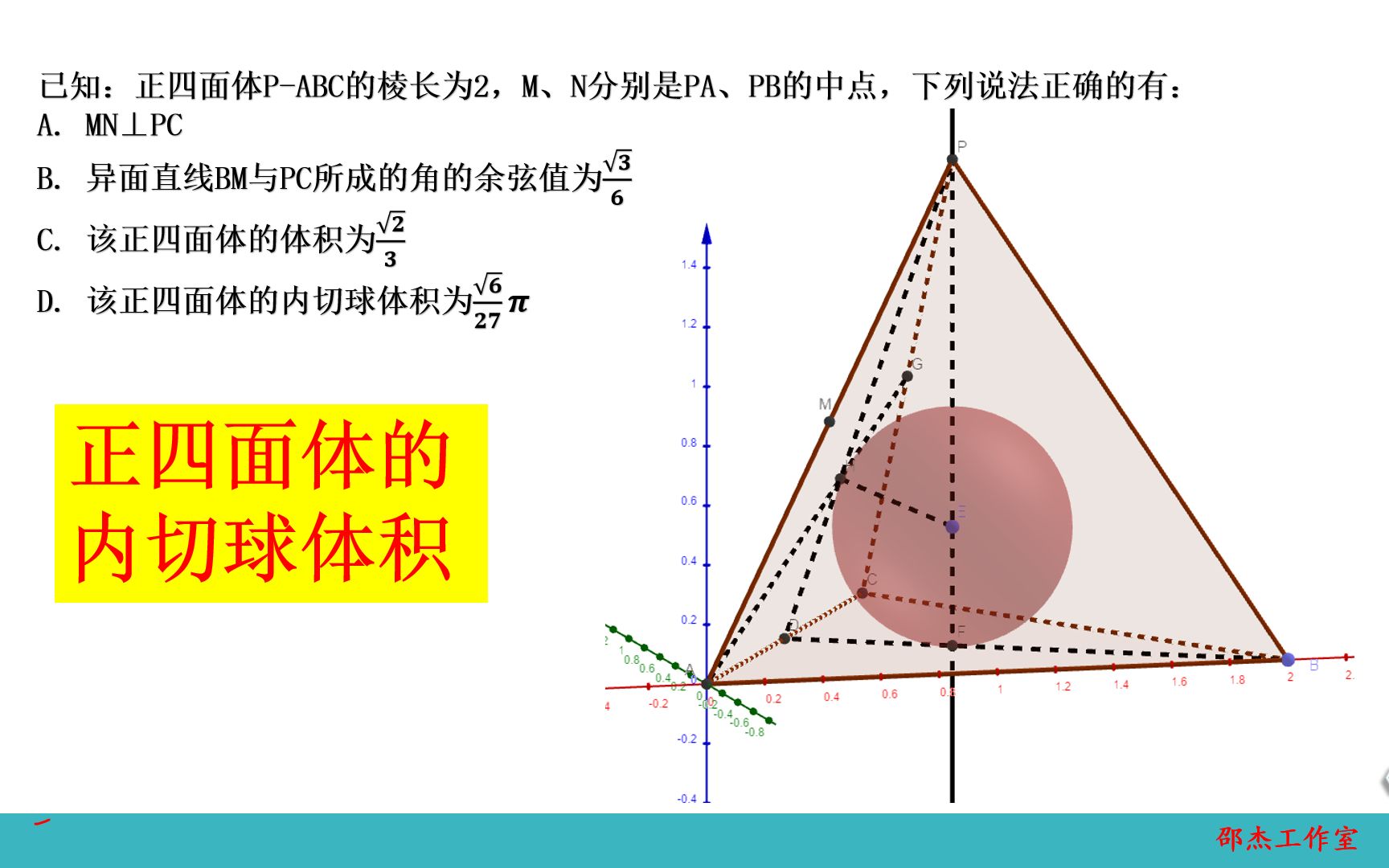
正四面体的内切球体积
图片尺寸1728x1080
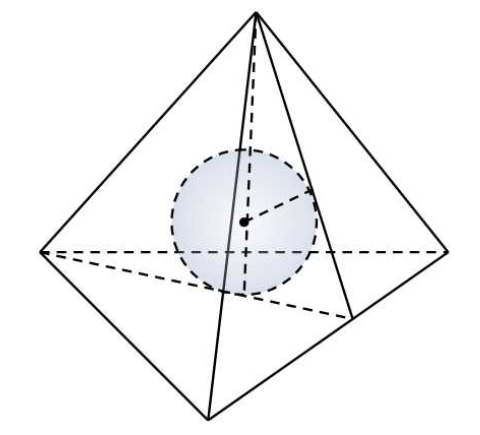
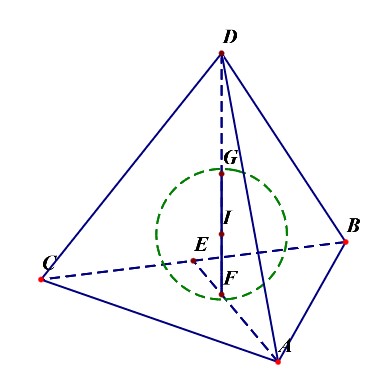
正四面体内切球
图片尺寸1080x810
正四面体的棱长为a,则其高为h=√6a3;正四面体的内切球球心,棱切球球
图片尺寸408x399
小高老师正四面体内切球的半径两种求法几何法解向量数量积最值问题
图片尺寸2304x1444
正四面体的内切球球心到一个面的距离等于这个正四面体高的
图片尺寸252x249
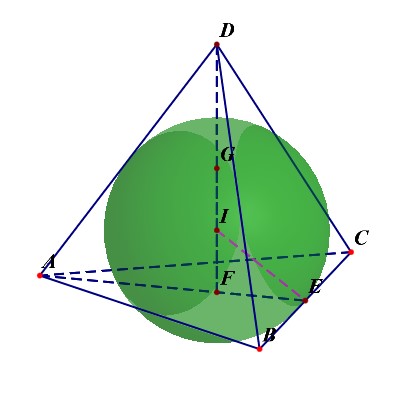
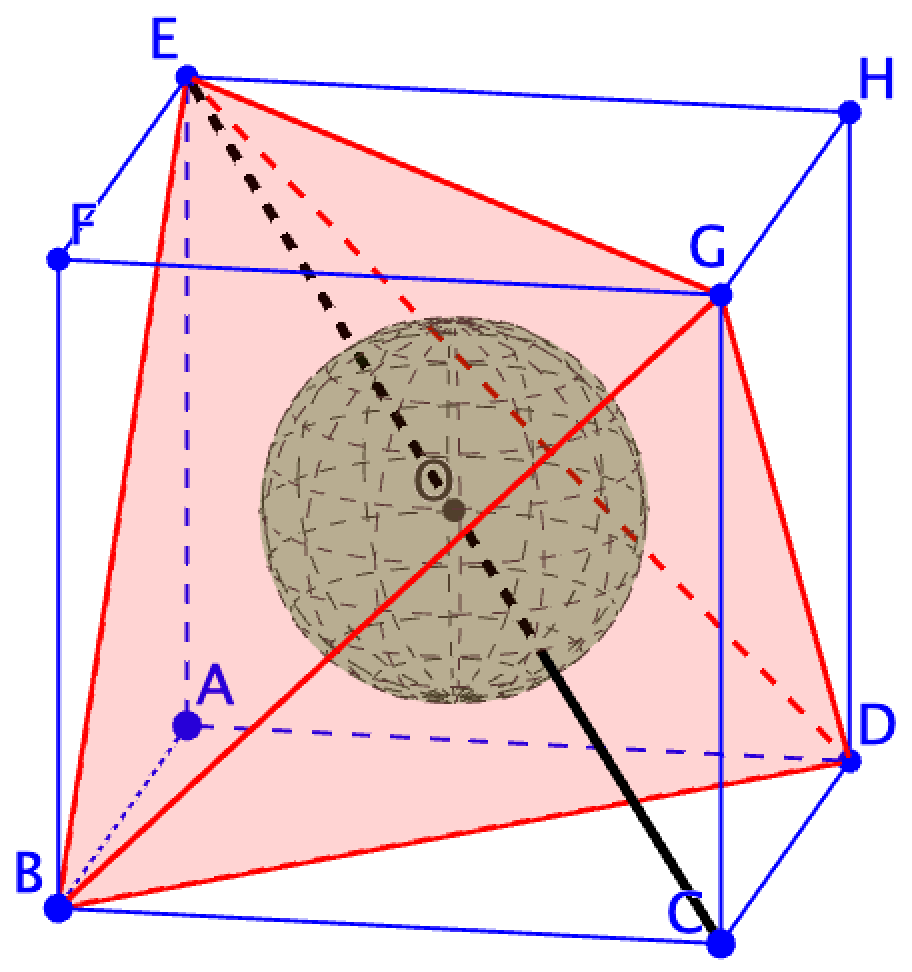
正四面体的外接球与内切球
图片尺寸736x793
正四面体的棱切球-补图法
图片尺寸450x253
正四面体的内切球半径(r_{内}=cfrac{sqrt{6}a}{12}=cfrac{1}{4}h=if)
图片尺寸390x380
正四面体内切球和外接球(好用)ppt模板
图片尺寸1200x3575
为什么正四面体的内切球半径为正四面体高的1/4
图片尺寸367x256
求正四面体的内切球与外接球的体积比
图片尺寸378x352
立体几何之球问题
图片尺寸912x972
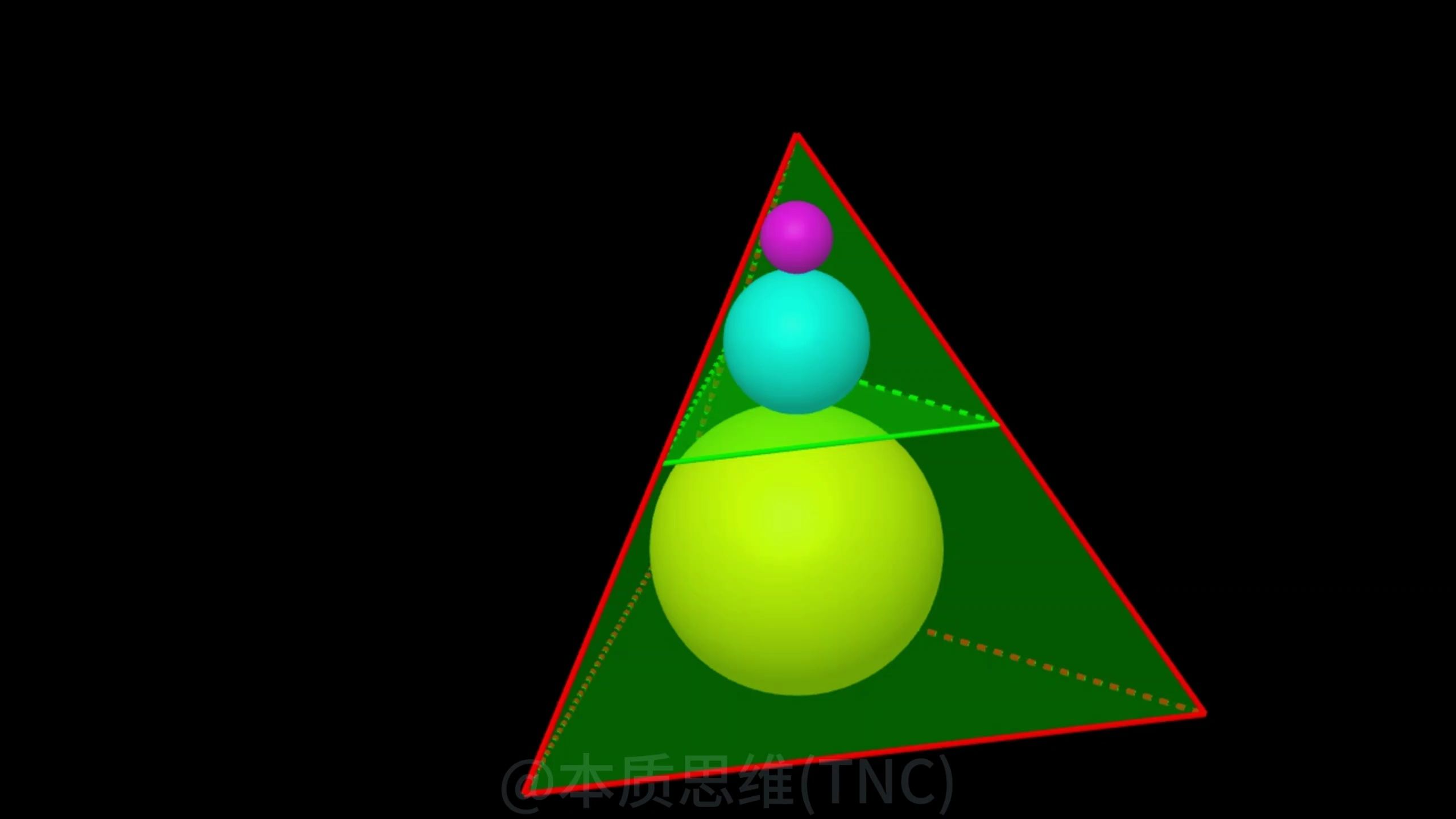
解析:例4,将半径都为1的四个钢球完全装入形状为正四面体的容器里
图片尺寸640x413
正四面体内切球
图片尺寸2560x1440
例2:求棱长为a的正四面体的外接球,棱切 球,内切球的体积之比.
图片尺寸1080x810
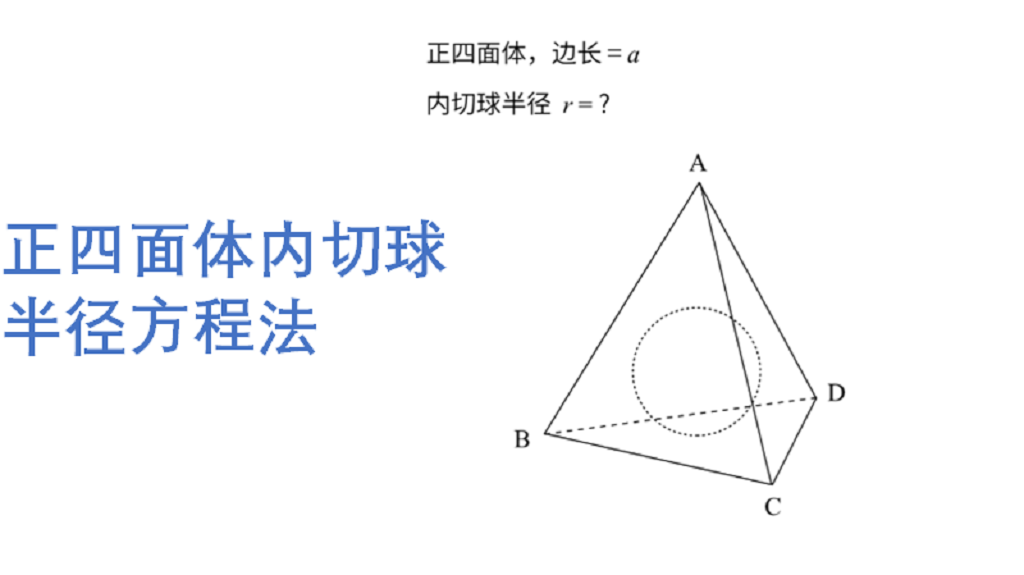
正四面体内切球半径方程法
图片尺寸1024x575
在棱长为6的正四面体内有一个内切球(球与正四面体的四个面都相切)
图片尺寸500x281
例3 棱长为2√3的正四面体内切一球,然后在正四面体和该球形成的肯抖
图片尺寸457x298
猜你喜欢:圆锥内切球图片正方体外接球正四面体的内切球正四面体的棱切球图片正四面体内切球示意图正四面体内切球半径图正四面体棱切球图片正四面体的外接球图片正方体的内切球图片正四面体内切球正四面体内切球半径正四面体棱切球图示正四面体的棱切球正方体内切球图片正四面体的棱切球半径正四面体图片球内接正四面体四面体内切球正四面体的外接球正四面体内切圆正四面体和三角锥图片正方体的内切球正三棱锥的内切球正方体棱切球图片正方体的外接球图片正方体内切球圆的内切和外切图片正四面体展开图甲烷的正四面体结构图正四面体的性质梁洁图片最新图片辣姜子卡地亚手表塔克系列吴鹤汀书画QQ订阅号图标库劳小奏鸣曲op20no1四川坝坝席偶像活动Planet鱼缸氧气泵结构声呐赶鱼器房颤抗凝我走后歌词